- Fabrizio Ottati
- 2023, Dec 26
NorthPole is the new shiny artificial intelligence (AI) accelerator developed by IBM.
NorthPole, an architecture and a programming model for neural inference, reimagines (Fig. 1) the interaction between compute and memory by embodying 10 interrelated, synergistic axioms that build on brain-inspired computing.
The creators claim that NorthPole design has been driven by 10 axioms inspired by human biology. We will use them as guidelines to analyze the paper, keeping the same outline as the original article.
Axiomatic design
Axiom 1 - A dedicated DNN inference engine
Turning to architecture, NorthPole is specialized for neural inference. For example, it has no data-dependent conditional branching, and it does not support training or scientific computation.
NorthPole is an application specific integrated circuit (ASIC): it can run only
deep neural networks (DNNs). Regarding “no data-dependent conditional
branching”, it means that the “code” it is able to run has no conditional
branches: it is a pure sequence of instructions, to be executed one after the
other, and pre-defined, as it should be when you are performing matrix
multiplications, i.e., running neural networks. There are no branches with
data-dependent ifs.
This is extremely important, because engineers have spent a lot of time making branches impact on performance minimum, especially in superscalar processors that have to deal with any possible code being compiled for them. For more information on this, the reader is referred to Computer architecture , by Hennessy, Patterson and Asanovic. If the code being run does not contain any of these conditional statements, there is no need for supporting them in hardware, which also gives a lot of space to optimizations in the dataflow.
Moreover, NorthPole is an inference-only accelerator, i.e., you cannot train a DNN on it, but only run it in inference. Training efficiency and speed is important, but inference costs cannot be ignored: for instance, consider that at the current moment each ChatGPT inference costs 0.04$ to OpenAI [Semianalysis ] to run in the cloud, just taking into account the number of machines and the electricity needed to power them and keep them cool.
Things change if you take into account the sparsity of the data inside a neural network, i.e., that layers in DNNs output a lot of zeros; since multiplying by zero a number is useless, a smart strategy would be to skip all the operations with zeros involved. To put this in code terms:
def dot_prod(a: torch.Tensor, b: torch.Tensor) -> torch.Tensor:
res = torch.Tensor([0])
for i in range(len(a)):
a_i, b_i = a[i], b[i] # Reading the inputs.
res += a_i * b_i # When either a[i]==0 or b[i]==0, you are accumulating zeros,
# which is useless.
return res
def dummy_sparse_dot_prod(a: torch.Tensor, b: torch.Tensor) -> torch.Tensor:
res = torch.Tensor([0])
for i in range(len(a)):
a_i, b_i = a[i], b[i] # Reading the inputs.
if a_i != 0 and b_i != 0:
res += a_i * b_i # Now all the zeros are being skipped.
return res
It seems easy, isn’t it? Well, it is not. The if in dummy_sparse_dot_prod is
a mess. Why so? Well, the problem is that when this code is running in
hardware, the line a_i, b_i = a[i], b[i] is much more costly (i.e., it takes
more energy to execute it) than a_i * b_i
[Horowitz
]! This is due to how
we design our digital circuits to perform these operations. Hence, what you
would like to avoid is to read the inputs, more than to multiply them! Hence, if
to check that these are not zero you need to read them, well, you have lost the
game :)
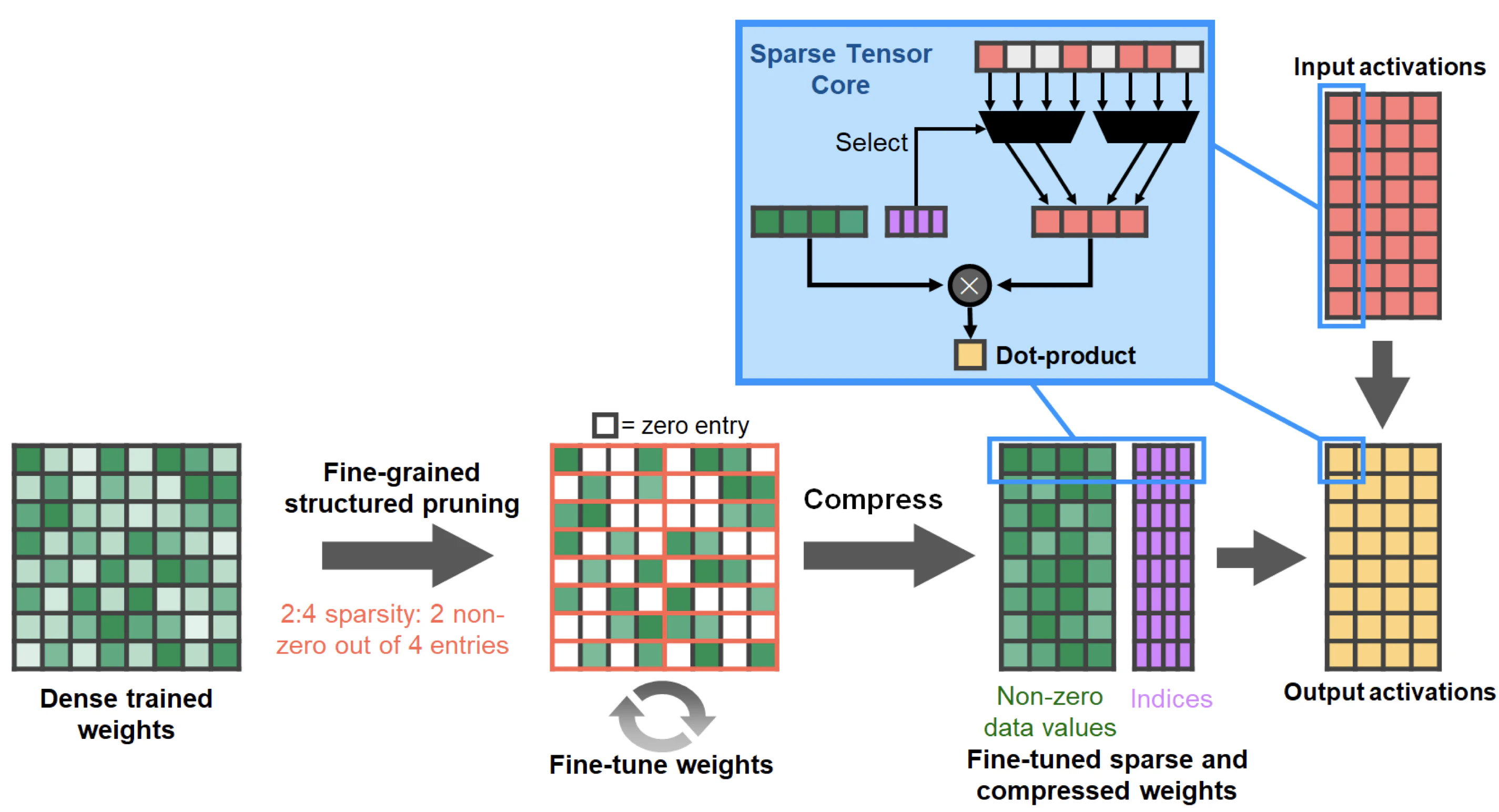
When you want to skip zero-computations, you need to introduce a structured approach (i.e., the zeros distribution in the matrices cannot be random, but it has to follow a structure) if you want to improve performance using sparsity [Wu et al. ], which means reading and processing only non-zero samples. For instance, Nvidia graphics processing units (GPUs) support 2:4 sparsity, which means that every 4 elements in a matrix, 2 are zeros (more or less, I am not being extremely precise on this).
Axiom 2 - Getting inspired by biological neurons
Inspired by biological precision, NorthPole is optimized for 8, 4, and 2-bit low-precision. This is sufficient to achieve state-of-the-art inference accuracy on many neural networks while dispensing with the high-precision required for training.
Neurons in biology communicate by means of voltage spikes. These can interpreted as binary signals: if I have a spike, I have a logic one; if there is no spike, I have a logic zero. This information encoding, if implemented in hardware, requires a single bit. This is the analogy the authors are referring to.
Why should I care about the precision of the data in my neural network? Let’s introduce a couple of concepts.
By precision it is meant the number of bits to which your data is encoded. The larger this number is, the larger numbers you can describe with your bit word, but also smaller since some of those bits are used to encode the decimals. However, you cannot use a large number of bits for each datum: first, because it would require much more memory to host these data; second, it requires much more energy to process them!
| Operation | Floating point energy [pJ] | Integer energy [pJ] | Energy ratio FP/INT |
|---|---|---|---|
| Addition | 0.4 (16 b), 0.9 (32 b) | 0.03 (8 b), 0.1 (32 b) | ~13.3x (16 b / 8 b), 9x (32 b / 32 b) |
| Multiplication | 1.1 (16 b), 3.7 (32 b) | 0.2 (8 b), 3.1 (32 b) | 5.5x (16 b / 8 b), ~1.2x (32 b / 32 b) |
In the table above [Horowitz
],
the energy required to perform addition on ints and floats is provided. You
could notice that it is much more convenient to work with ints! This is due to
the fact that the physical hardware required to perform floating point
arithmetic is much more complex that the corresponding integer one. That is
why we want to represent our DNNs weights and activations with integers!
However, you cannot simply convert an integer to a floating point value. For instance, the number 1.2345 would become 1 as an integer. This means that you would degrade the information encoded in the data, and the network would not perform as expected, showing a large loss in accuracy. For this reason, researchers have come up with quantization algorithms: these allow to convert floating point values to integer ones while loosing as few information as possible in the process. Since some information is lost in any case, the DNN usually needs to be retrained a bit using its integer version in order to recover the loss in performance.
We have been running DNNs using INT8 since ~2017 without claiming biological inspiration. Recently, however, progress has been made and we can use INT4 quantization (only 4 bits to represent a number) with marginal loss in performance compared to the 32-bit floating point (FP32) baseline that you trained on your GPU [Keller et al. ].
Moreover, FP16 precision is starting to be enough for training. State of the art GPUs are also supporting FP8 and integer precision [NVIDIA H100 Tensor Core GPU Architecture ].
Axiom 3 - Massive computational parallelism
NorthPole has a distributed, modular core array (16-by-16), with each core capable of massive parallelism (8192 2-bit operations per cycle) (Fig. 2F).
When claiming 8192 operations per clock cycle, using INT2 operands, it means that NorthPole is able to process 8192 numbers encoded to 2 bits every x nanoseconds. NorthPole uses a clock frequency of 400 MHz; hence, every 2.5 ns, it processes 8192 INT2 numbers.
However, NorthPole also supports INT4 and INT8 operands. This means that the underlying hardware must be reconfigurable. To understand this, we must figure out which is the fundamental operation implemented by modern deep learning accelerators (but not only): the multilply-and-accumulate (MAC) operation. Why do we care about MACs?
DNNs are basically matrix multipliers: a neural network receives a vector in input and multiplies it by a matrix of weights, producing in output another vector. The reader is referred to the awesome YouTube playlist created by 3Blue1Brown for more information on this.
Let us consider a naive matrix-vector multiplication.
def naive_mat_vec_mul(v: torch.Tensor, m: torch.Tensor) -> torch.Tensor:
m_rows, m_cols = m.shape
assert m_cols == len(v)
res = torch.zeros((m_rows,))
for r in range(m_rows):
for c in range(m_cols):
res[r] += v[c] * m[r, c] # Hey, this is multiplication and
# accumulation! Here's our MAC!
return r
As you can see, the MAC is the fundamental operation employed in a matrix-vector product. That’s why we care about it being implemented in hardware in the most efficient way.
Coming back to NorthPole MACs, we stated that these can process INT2, INT4 and INT8 operands. We also talked about reconfigurability. What does this mean? These MACs can be configured in single-instruction-multiple-data (SIMD) mode, i.e., you can “glue” together 4 INT2 operands to form an INT8 word and work on these in parallel.
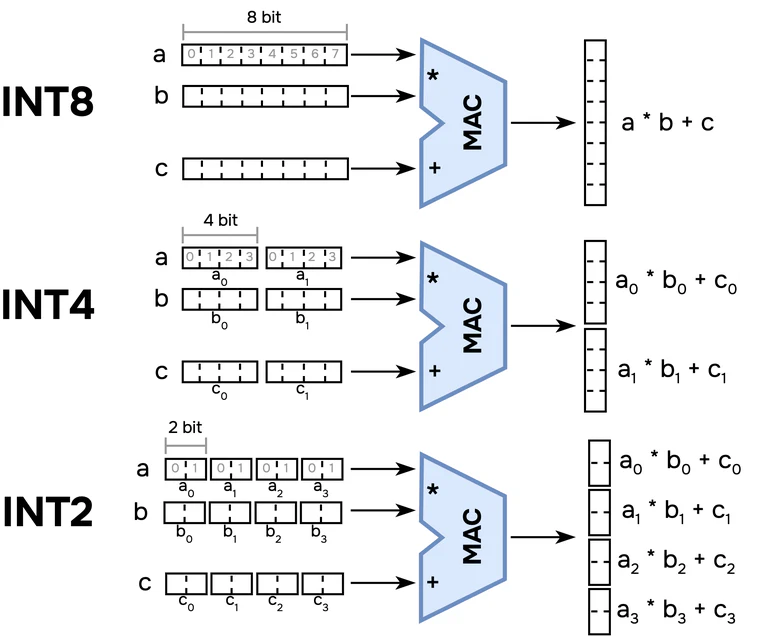
Above it is shown a visual description of how this parallelism is exploited. The total word width is always 8 bit, but more values can be glued together to be processed in parallel in the MAC, which produces more outputs at once for the INT4 and INT2 precisions. This is why in the “Silicon implementation” section of the paper it is written:
NorthPole has been fabricated in a 12-nm process and has 22 billion transistors in an 800-mm2 area, 256 cores, 2048 (4096 and 8192) operations per core per cycle at 8-bit (at 4- and 2-bit) […]
Now, each NorthPole core has 256 of these units, and these work in parallel on different sections of the neural network layer being processed.
Cortex-like modularity of the tiled core array enables homogeneous scalability in two dimensions and, perhaps, even in three dimensions and is also amenable to heterogeneous chiplet integration.
Regarding the cortex-like modularity, here I can only guess. Deep neural networks have been inspired by the cortex, since this is a multi-layer structure in which information is passed among layers. Each layer performs a certain function, like in deep convolutional neural networks: the first layers extract high level features (e.g., edges), while the deep layers combine this information to get something useful out of it.
Axiom 4 - Efficiency in distribution
NorthPole distributes memory among cores (Figs. 1B and 2F) and, within a core, not only places memories near compute (2) but also intertwines critical compute with memory (Fig. 2, A and B). The nearness of memory and compute enables each core to exploit data locality for energy efficiency. NorthPole dedicates a large area to on-chip memory that is neither centralized nor organized in a tradi- tional memory hierarchy.
NorthPole is a spatial architecture, in contrast to GPUs and TPUs that are temporal architectures [Sze et al. ]: this means that instead of having a single on-chip memory that all the PEs share, (part of) memory is co-located with the processing units. For more information about GPUs, I suggest this excellent blog written by Abhinav Upadhyay .
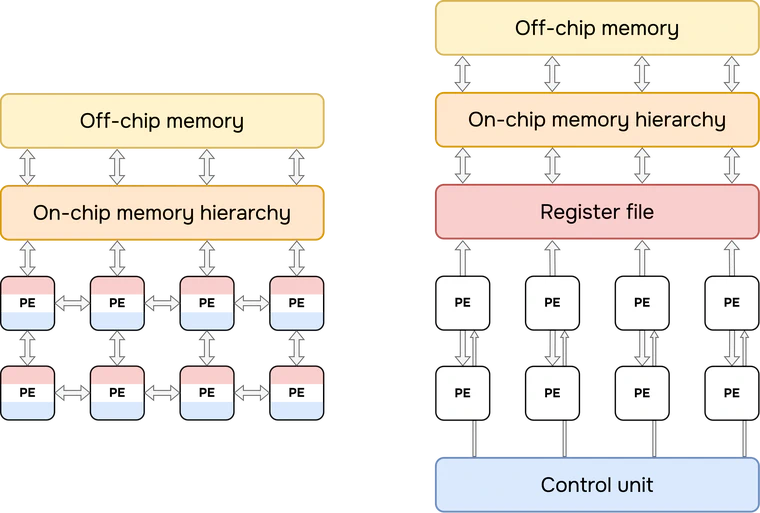
Eyeriss [Chen et al. ] proposed this approach and taxonomy in 2016. Field programmable gate arrays (FPGAs) have been doing this since the beginning, with distributed SRAM near the logic or the special purpose macros available on the silicon. I do not know if it is brain-inspired but it makes sense from a silicon perspective if you want to maximize efficiency.
Axiom 5, 6 - A neural Network-on-Chip
NorthPole uses two dense networks on-chip (NoCs) (20) to interconnect the cores, unifying and integrating the distributed computation and memory (Fig. 2, C and D) that would otherwise be fragmented. These NoCs are inspired by long-distance white-matter and short-distance gray-matter pathways in the brain and by neuroanatomical topological maps found in cortical sensory and motor systems (21). One gray matter–inspired NoC enables spatial computing between adjacent cores (Fig. 3 and fig. S1). Another white matter–inspired NoC enables neuron activations to be spatially redistributed among all cores. Another two NoCs enable reconfiguring synaptic weights and programs on each core for high-speed operation of compute units (Fig. 2, C and D). The brain’s organic biochemical substrate is suitable for supporting many slow analog neurons, where each neuron is hardwired to a fixed set of synaptic weights. Directly following this architectural construct leads to an inefficient use of inorganic silicon, which is suitable for fewer and faster digital neurons. Reconfigurability resolves this key dilem- ma by storing weights and programs just once in the distributed memory and reconfiguring the weights during the execution of each layer using one NoC and reconfiguring the programs before the start of the layer using another NoC. Stated differently, these two NoCs serve to substantially increase (up to 256 times, in some cases) the effective on-core memory sizes for weights and programs such that each core computes as if the weights and program for the entire network are stored on every core. Consequently, NorthPole achieves 3000 times more computation and 640 times larger network models than TrueNorth (14), although it has only four times more transistors (supplementary text S1).
Take-home message: PEs communicate using dedicated busses, in what is called a network-on-chip (NoC). There are two NoCs in NorthPole: one to exchange the intermediate results among PEs (the gray matter NoC), one for the inputs of the neural network (the white matter). Two more NoCs, to load the weights to the PEs and the instructions to be performed (i.e., the sequence of operations to be carried out). The comparison with TrueNorth is not really fair: completely different designs, completely different goals.
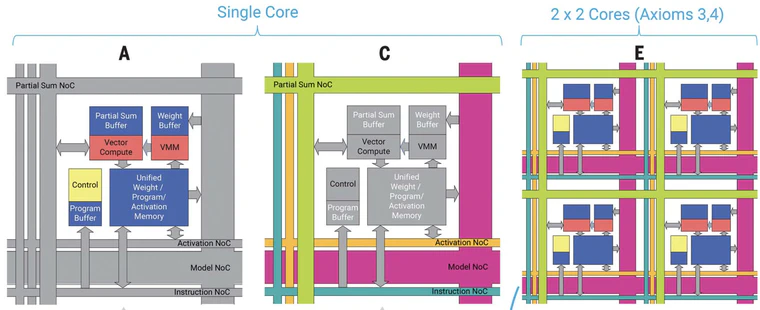
NortPhole architecture is summarized above. Each core has memory structures named buffer to host locally weights, inputs and partial results of the matrix multiplication being performed (figure A). In figure C, the different NoCs are highlighted: the partial sums NoC distributes the partial results among cores (refer to the layer-fuse architecture); the activation NoC carries inputs and layers outputs; the instruction NoC is used to tell the sequence of instructions to be carried out by the core; the model NoC is the one that trasnfers the layers weights to the computational cores.
In my opinion, the instruction core plays an important role. Having a specialized instruction set architecture (ISA) has a large impact on performance.
| ISA operation | Energy [pJ] | Energy overhead (instruction decoding / computation) |
|---|---|---|
| HFMA | 1.5 | 20x |
| HDP4A | 6 | 5x |
| HMMA | 110 | 0.22x |
| IMMA | 160 | 0.16x |
Above it is a table considering the ISA of Nvidia GPUs chip [William J. Dally ]. The ISA instruction correspond to a matrix multiplication core operation, roughly. The total energy associated to each operation is displayed, together with the ratio between the energy dedicated to instruction decoding (understand what you need to do, prepare operands fetching) and the actual computation being carried out.
The instruction HFMA stands for half-precision (FP16) fused multiply-add: with
a single instruction, basically, you perform an FP16 MAC. This leads to an
overhead of 20x when you need to execute all these instruction to multiply two
matrices, as it happens in deep learning workloads. All this energy is wasted
because you need to tell the hardware what to do at each matrix entry, instead
of telling it “Just multiply these two matrices, please.”.
For HDP4A, the instruction performs a dot product between vectors of 4
elements, and then accumulate. This was introduced in the Nvidia Volta
architecture: tensor cores were introduced, which translates into having
specialized ISA instruction to perform full matrix multiplication (of small
matrices, of course, like 4x4). In fact, HMMA stands for half-precision
matrix multiply and accumulate: with a single ISA instruction, a (small) matrix
multiplication is performed, hence you minimize the overhead of the control
logic. In the Turing architecture, the integer cores were introduced: IMMA
stands for integer MMA, which provides even better performance as you do not
have to deal with the floating point format. In this, two 8x8 matrices in INT8
precision are multiplied together.
We can expect NorthPole to do something similar at the low level of the software stack, in order to achieve that outstanding efficiency.
Axiom 7 - No branches, lots of fun!
NorthPole exploits data-independent branching to support a fully pipelined, stall-free, deterministic control operation for high temporal utilization without any memory misses, which are a hallmark of the von Neumann architecture. Lack of memory misses eliminates the need for speculative, nondeterministic execution. Deterministic operation enables a set of eight threads for various compute, memory, and communication operations to be synchronized by construction and to operate at a high utilization.
This comes from the fact that NorthPole is running neural networks: if you know
exactly which operations will be performed, with no branching in your program
(i.e., no ifs), and all the data is as close as possible to the PEs, and
data movement is fully deterministic (e.g., first I process the channel
dimension, then the width, then the height etc.), I would be very worried if I
had stalls or cache misses :)
Axiom 8 - Low precision, same performance with backprop
Turning to algorithms and software, co-optimized training algorithms (fig. S3) enable state-of-the-art inference accuracy to be achieved by incorporating low-precision constraints into training. Judiciously selecting precision for each layer enables optimal use of on-chip resources without compromising inference accuracy (supplementary texts S9 and S10).
In short: IBM will provide a quantization aware training (QAT) toolchain with the NorthPole system. QAT starts, usually, from a full precision FP32 model and converts all the weights and activations to integers, in order to reduce their precision. This leads to information loss that worsens the accuracy of the network: to recover this, the DNN is trained for few more epochs to use backprop to tune the network taking into account the approximations brought by the quantization process.
Axiom 9 - Start optimizing inference from the code
Codesigned software (fig. S3) automatically determines an explicit orchestration schedule for computation, memory, and communication to achieve high compute utilization in space and time while ensuring that there are no resource collisions. Network computation is broken down into layers, and each layer computation is spatially mapped to the core array. To minimize long-distance communication, spatial locality of neural activations is maintained across layers when possible. To prevent resource idling, core computation and intra and intercore data movement are temporally synchronized so that data and programs are present on each core before use. Together, algorithms and software constitute an end-to-end toolchain that exploits the full capabilities of the architecture while providing a path to migrate existing applications and workflows to the architecture.
So, they will provide a quantization aware training framework for DNNs, and they state that the dataflow of the accelerator is optimized to maximize efficiency. Eyeriss [Chen et al. ] strikes again.
Axiom 10 - What happens in NorthPole, stays in NorthPole
NorthPole employs a usage model that consists of writing an input frame and reading an output frame (Figs. 1D and 3), which enables it to operate independently of the attached general processor (16). Once NorthPole is configured with network weights and an orchestration schedule, it is fully self-contained and computes all layers on-chip, requiring no off-chip data or weight movement. Thus, externally, the entire NorthPole chip appears as a form of active memory with only three commands (write input, run network, read output), with the minimum possible input-output bandwidth requirement; these features make NorthPole well suited for direct integration with high-bandwidth sensors, for embedding in computing and IT infrastructure, and for real-time, embedded control of complex systems (22).
In short, the network is hosted completely on the chip, and you pass the inputs via PCIe to the chip, wait some time and read back the result. On the point of energy efficiency: they write the following.
[…] these features make NorthPole well suited for direct integration with high-bandwidth sensors, for embedding in computing and IT infrastructure, and for real-time, embedded control of complex systems (22).
Uhm, real-time embedded system. So it must be super efficient to be run on such a limited system, right? However, in Table 1 of the paper, the power consumption required to run an INT8 version of ResNet50 is 74 W. Ouch :)
Silicon implementation
NorthPole has been fabricated in a 12-nm process and has 22 billion transistors in an 800-mm2 area, 256 cores, 2048 (4096 and 8192) operations per core per cycle at 8-bit (at 4- and 2-bit, respectively) precision, 224 megabytes of on-chip memory (768 kilobytes per core, 32-megabyte framebuffer for input-output), more than 4096 wires crossing each core both horizontally and vertically, and 2048 threads.
Each core can carry out 2048 INT8 operations in parallel per iteration, which means that are 2048 PEs per core. Pay attention to the on-chip memory capability: 768 kB per core! That is a lot of memory. To understand how much, you can consider a neural network in which each parameter (for simplicity, weights only) is stored as INT8, occupying 1 B in memory. This means that a network with 768 k parameters can be hosted on a single core (forgive me, it is not fully precise as I am considering only the weights).
Energy, space and time
For methodological rigor that ensures a fair and level comparison of various implementations, it is critical that all evaluation metrics be independent of the details of the implementations, which can vary arbitrarily across architectures at the discretion of the designers. The architecture-independent goodness metric adopted here is that all implementations must be measured at state-of-the-art inference accuracy.
The authors consider the data from other papers in which they used the data format (FP, INT) that gives the highest accuracy on the network being run on the chip, to ensure fair comparison.
The architecture-independent cost metrics adopted here are now introduced. Turning first to energy, different integrated- circuit (IC) implementations have different throughputs (in frames per second (FPS)) at different power consumptions (in watts). Therefore, FPS per watt (equals frames per joule) is a widely used energy metric for comparing ICs.
To measure efficiency on image classification tasks, the author consider how many inferences you can run on the accelerator using only one joule of energy. Here, I will consider only two GPUs from Nvidia and NorthPole, because that is the most interesting comparison. The DNN being used is a ResNet50, and it is benchmarked on ImageNet.
| Accelerator | Power [W] | Throughput (FPS) | Efficiency [inferences / J] | Data format | Only DNNs? | Training? |
|---|---|---|---|---|---|---|
| Nvidia A100 | 400 | 30,814 | 80 | FP32,16; INT8 | ✘ | ✔ |
| Nvidia H100 | 700 | 81,292 | 116 | FP32,16; INT8,4 | ✘ | ✔ |
| NorthPole | 74 | 42,460 | 571 | INT8,4,1 | ✔ | ✘ |
Northpole is winning! And by a lot! This is mostly due to the fact that A100 and H100 are really power-hungry devices (look at the power consumption!) and you can use them to run any model you want, also for training in FP32 and FP16. NortPole, instead, is meant only for inference of quantized (i.e., INT8 parameters) neural networks.
Moreover, the GPUs being considered use large amount of off-chip (hence, energy-hungry) memory to deal with any kind of DL workload being run on them. Hence, most of the inefficiency is due to the large energy consumption associated to retrieving data from external DRAM. In fact, the authors write:
Even relative to the H100 GPU, which is implemented using a 4 nm silicon process node, NorthPole delivers five times more frames per joule. NorthPole has high energy efficiency because of less data movement, which is enabled by a lack of off-chip memory, the intertwining of on-chip memory with compute, the locality of spatial computing, and a better use of low-precision computation.
Moreover:
All compared architectures implement considerably faster clock rates than NorthPole, and yet NorthPole outperforms on the space metric by achieving substantially higher instantaneous parallelism (through high utilization of many highly parallel compute units specialized for neural inference) and substantially lower transistor count owing to low precision (Fig. 4B).
NorthPole runs at 400 MHz while an A100 GPU can run up to 1.4 GHz. Of course, GPUs have much more “redundant” hardware to be programmable for more tasks. Hence, is it fair this comparison with general purpose hardware? Sure. However, shall we call in a fairer competitor ? :)
| Accelerator | Power [W] | Throughput (FPS) | Efficiency [inferences / J] | Data format | Only DNNs? | Training? |
|---|---|---|---|---|---|---|
| Nvidia A100 | 400 | 30,814 | 80 | FP32,16; INT8 | ✘ | ✔ |
| Nvidia H100 | 700 | 81,292 | 116 | FP32,16; INT8,4 | ✘ | ✔ |
| NorthPole | 74 | 42,460 | 571 | INT8,4,1 | ✔ | ✘ |
| Keller et al. | N/A | 212 | 4714 | INT8,4 | ✔ | ✘ |
The competitor (Keller et al.) is a chip developed by Nvidia and published in 2022 at ISSCC. The data are taken from the JSSC journal version of the paper. A big disclaimer: the measurements come from a tapeout of Nvidia, i.e., they have designed a new accelerator and produced a test chip, and then they have run a neural network on it and measured performance. It is not (yet) a plug-in accelerator like NorthPole. This explains why the throughput is so low and the efficiency so high.
The Nvidia accelerator is meant for inference only, just like NorthPole, and it uses a very advanced quantization technique [Dai et al. ] to use INT4 precision without compromising accuracy. Moreover, the accelerator is designed to run large Transformers on it, but I have used their ResNet50 data for fair comparison with NorthPole. Like NorthPole, it is an inference-only accelerator.
(My) conclusions
In conclusion, the following statement
Inspired by the brain, which has no off-chip memory, NorthPole is optimized for on-chip networks […]
will make me sleep better tonight, knowing that I do not have a DDR4 stick on top of my head :)
NorthPole is a super-interesting experiment: it is an extremely large accelerator, with a distributed memory hierarchy that allows extreme efficiency when parallelizable workloads, such as DNNs, are targeted. Regarding the brain inspiration, I do not know if calling NoCs white or gray matter is enough, and I do not think it matters at all! In my opinion, NorthPole is an excellent engineering work, that takes into account key factors:
- reduced precision operations are much more efficient that high-precision ones. An FP32 multiplication costs much more than an INT8 one.
- DNNs are extremely robust to quantization, and with INT8 precision there is basically no accuracy degradation.
- memory accesses are much more costly than computations when going up the memory hierarchy (i.e., external DRAMs and so on).
However, this brain-inspired approach seems to prove more useful than other ones at the moment, such as spiking networks accelerators: the distributed memory hierarchy leads to great improvement in processing efficiency, without compromising network performance on the selected tasks (object detection and recognition in the NorthPole paper).
I can see clusters of NorthPole being stacked in servers to improve inference efficiency (see the OpenAI case). It is not, in my opinion, an edge computing solution. I wish there where more technical details in the paper, since it is more on the divulgative side.
Acknowledgements
I would like to thank Jascha Achterberg for reviewing this blog post and the super-useful discussion about the brain-inspired traits of NorthPole: he convinced me that the way in which the authors claim biology inspiration actually proves useful (e.g., distributed memory hierarchy), differently from other approaches that severly compromise performance (e.g., accuracy), with negligible efficiency improvements.
I would also like to thank Siddharth Joshi for pointing out that Keller et al. does not directly support sparsity in hardware, contrarily to what I believed.
Bibliography
- Neural inference at the frontier of energy, space, and time , Dharmendra S. Modha et al., Science, 2023.
- HighLight: Efficient and Flexible DNN Acceleration with Hierarchical Structured Sparsity , Yannan Nellie Wu et al., IEEE Micro, 2023.
- A 95.6-TOPS/W Deep Learning Inference Accelerator With Per-Vector Scaled 4-bit Quantization in 5 nm , Ben Keller et al., IEEE Journal of Solid State Circuits (JSSC), 2023.
- Computing’s energy problem (and what we can do about it) , Mark Horowitz, IEEE International Solid-State Circuits Conference (ISSCC), 2014.
- NVIDIA H100 Tensor Core GPU Architecture , Nvidia, 2023.
- LoopTree: Enabling Exploration of Fused-layer Dataflow Accelerators , Michael Gilbert et al., IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), 2023.
- Efficient Processing of Deep Neural Networks: A Tutorial and Survey , Vivienne Sze et al., IEEE Proceedings, 2017.
- VS-Quant: Per-Vector Scaled Quantization for Accurate Low-Precision Neural Network Inference , Steve Dai et al, Machine Learning and Systems (MLSys), 2021.
- What Every Developer Should Know About GPU Computing , Abhinav Upadhyay, 2023.
- Hardware for deep learning , William J. Dally, HotChips 2023.